Labur: Lerrootakoa ariketa da: erantzun gehien eragin dituzten galderak identifikatzea izan da helburua. Bilaketa horretan gehien kontzeptuaren inguruko analisi ariketa egiten da. Ikuskera matematikoan ardaztu nahi izan dut ariketa zati honetan, horregatik interesaren fokoa eta azalpenak galderetan kokatu dira.
Datuak
Lan hau egiteko oinarritzat Euskal Herri Hizkeren Atlaseko (EHHA hemendik aurrera) (Dialektologia batzordea 2008) lehenengo 44 galderen erantzunak erabili dira informatzaileek emandako formen edo lemen araberako alderaketa egin ahal izateko. EHHA I eta IIko datuak erabili dira formaren araberako alderaketarako soilik, ez baitigu denak izan lematizatuta eskura.
Denera 145 herritako datuak batu eta analizatu dira. Hori zati bitan banatuta egin da. Lehenengo azterketan alderatu nahi izan dira erantzunak ikuspegi bitatik: Erantzun lematizatuak eta lematizatu gabeko erantzun gordinetan, batutako formen araberakoa, alegia. Hori egin ahal izateko azpitalde bat egin da zeinetan batutako erantzun guztiak lematizatuta ere baitauden.Horretan denera 9481 forma batu dira, lematizazio prozesuaren ondoren 9129 unitate zenbatzen dira. Aurkezten den lehenengo alderaketa horretan helburu nagusi bi dira; bata bestearen menpekoa: elementuaren (galderaren edo herriaren) barne bariazioa aztertzea eta barne bariazio hori zehazteko adierazleak identifikatzea.
Beste ikuspegi posible batean, datu base osoa har liteke aztertzeko, eta ez soilik lematizatuta ditugun erantzunak. Horixe da hemen agertzen den bigarren azterketa; horretan datuen portaera aztertzen da, baina ezin konparatu litezke lematizatutako datuak lematizatu gabekoekin; beraz, deskribapen zabal eta herrena izango da bigarrena. Ikuskera horretan, datuek denera 26535 neurraldi dituzte eta batutako formen kopurua 37790koa da, 183 galderaren erantzunak aipatutako 145 herritan batuta.
Hurbilpena: datuen banaketara hurrerapena.
Hasierako azterketarako soilik hartu dira lematizatutako erantzunak dituzten kasuak; hau da, 44 galderaren erantzunak dira aztergai.
Bariaziorik handiena?
Bariazioaren handitasuna definitzeko orduan ikuskera egokiaren bila zenbait ikuskera ebaluatu behar dira.
- Gehieneko balioa zein elementutan hartzen da?
- Bataz beste, zein elementutan eman dira erantzun gehien?
- Muturreko balioak kenduta, zein elementutan eman dira erantzun gehien bataz beste?
- Zein da gehienetan emandako erantzun kopurua elementuan?
- Bataz besteko altuetatik, zeinek dauka desbiderapenik baxua?
- Banaketan alborapen negatiborik handiena duena?
Eta, elementu idazten dut, ikuskera matematikotik eragiketa bertsuak behar dituelako galderen araberako azterketak eta herrien araberakoak. Horrexegatik, lehenengo azterketa galderen arabera egiten da, maila gutxiagoko aldagaiak errealitatearen azterketa erraztu dezakeelakoan.
Azterketara hurbilpena
Datuen ulerkuntzarako grafikoak aztertuko dira. Lehenengokoa grafikoa datuen banaketa aztertzea da.
Galderen araberako azterketa
Hasierako ahalegina irudi sinple bat egitea da, galderak eta forma kopurua alderatuaz:
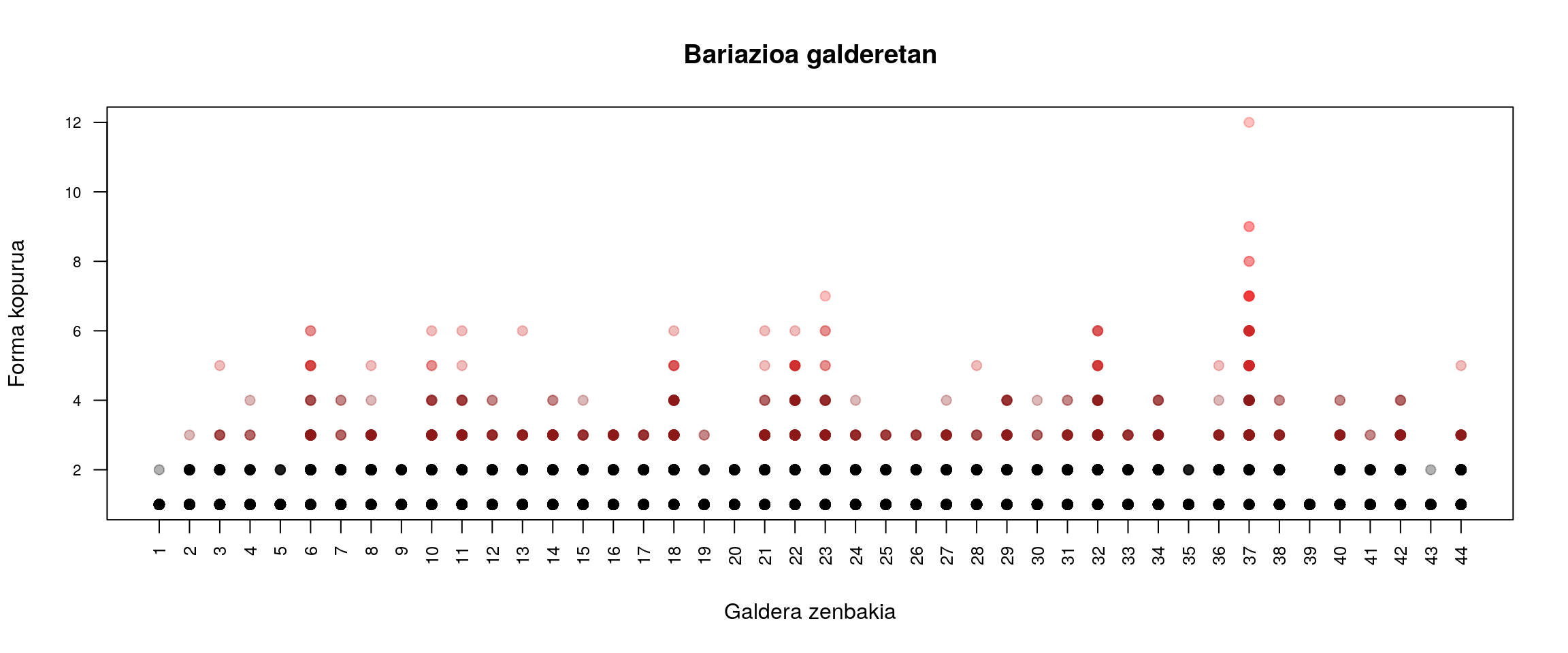
Irudian galdera bakoitzean batutako gehiengo erantzun kopurua argi ikusten da. Ikuskera horretatik argi dago 37. galderan batu direla erantzun gehien, 23.ean bigarren gehien eta hurrengoetan ez da argi ikusten zein alde dagoen, baldin eta badago, 6., 10., 11, 12,18, 21., 22, 23 eta 32.
Informazioa argitzeko ahaleginean, kutxa grafikoa erabili da bigarren pausuan. Kutxa grafikoak informazio asko eskaintzen du:
- Bitartearen tamaina
- Batez bestekoa
- Koartilak
- Outlierrak
Lehenengo galderaren erantzunen analisia 37. galderakoa da, irudiaren arbera horixe baita deigarriena.
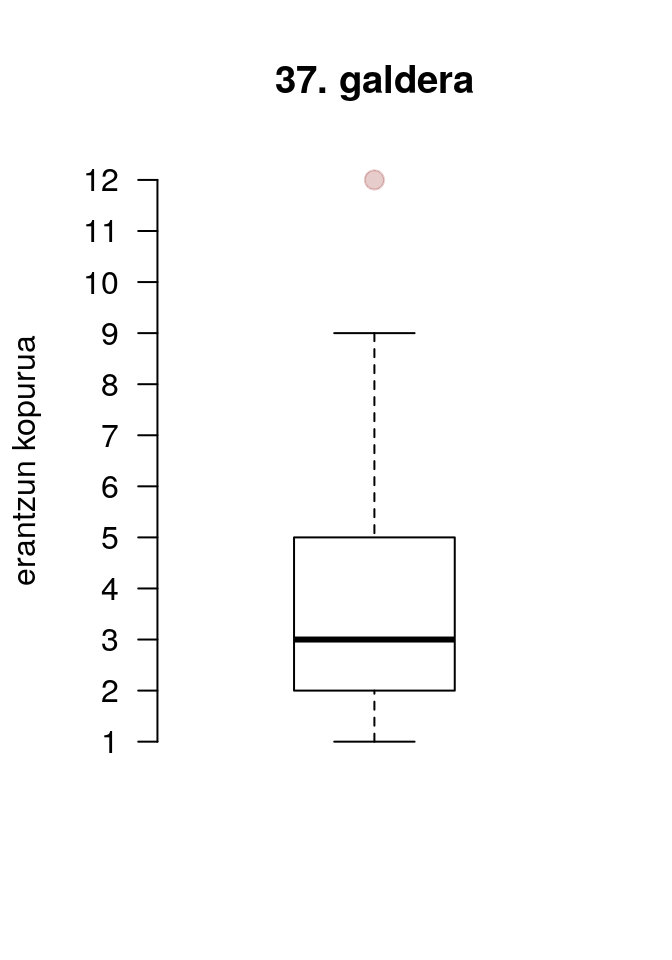
37. galderak, lehenengo grafikoan ikusi den moduan, erakusten du bariaziorik handiena. Batetik eta hamabi erantzun arte batu dira herri desberdinetan. Hamabi soilik kasu solteren batean (hamaika erantzunik ere ez da jaso-eta). Erantzun gehienak 1 eta 9 elementukoak izan dira. Aztertutako herrien aretean %25ean erantzun dira hiu eta bat elementuen artean, beste %25ek bi eta lau erantzun artean batu ditu, hurrengo %25 herritan hiru eta bost erantzunen arteko kopuruko erantzunak eman dituzte eta azken %25 5 eta 9 erantzunen artekoa da.
Bigarren pausotzat aztertzen dira antzerakoak ematen duten datuen portaerak, hobeto ulertze aldera. Helburu horretarako gorago aipatutako 8 galderen erantzun kopuruen portaera batera irudikatuko dugu.
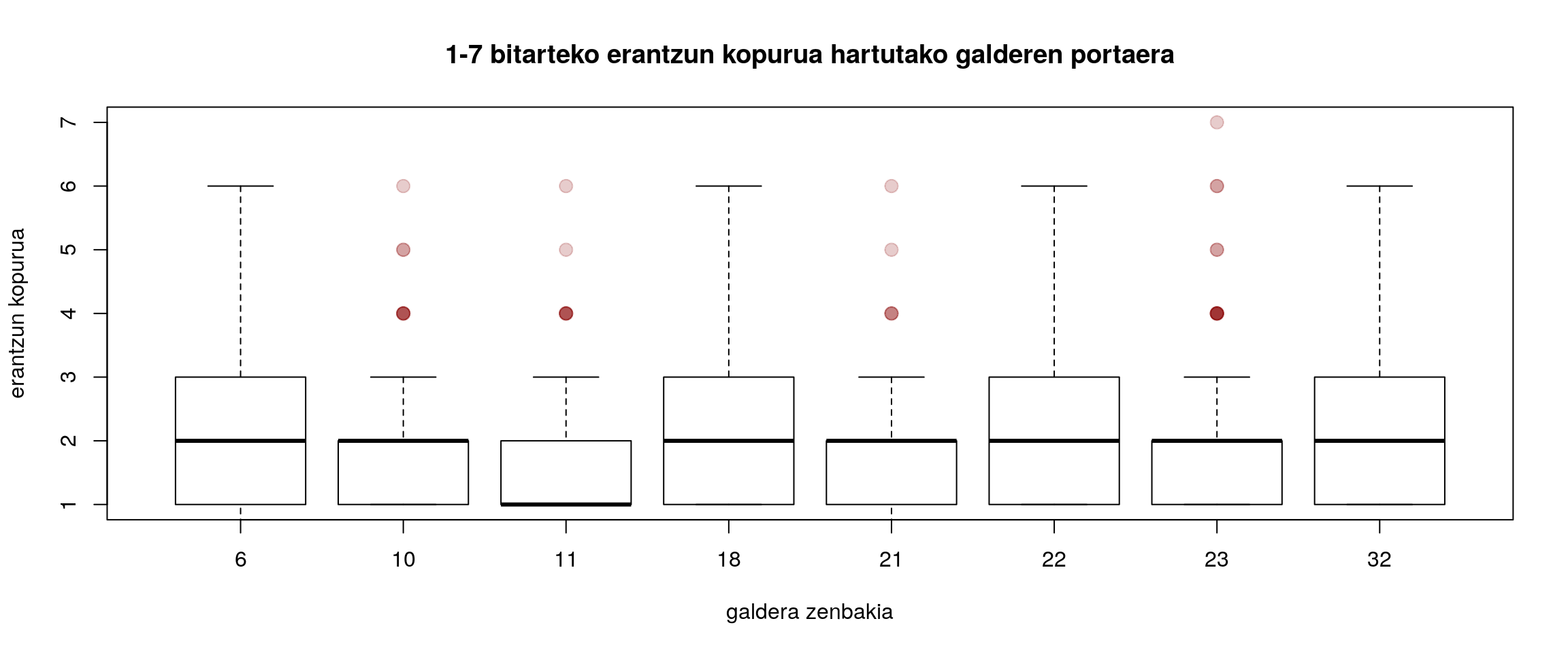
Irudiaren azterketan antzematen dira ezaugarri batzuk, bestean ezkutuan gelditzen izan direnak. Zortzi galdera horiek alderatu nahi baditugu barne-aldagarritasunari dagokionean, nahiz eta bitarte ia bera izan, ikus dezakegu portaera desberdina dutela:
- 10., 11., 21, eta 23. kasuetan 4 erantzun baino gehiago herri batzuetan batu badira ere, une puntualak direla ikusten da. Beraz, besteek bariazio handiagoa dutela esan genezake.
- Zehazki 11. galderan, gainera, batez besteko erantzun kopurua adierazten duen marra 1ean dago, beraz ondoriozta daiteke 10. 21. eta 23. galderek erantzun anitz gehiago eragin dituztela 11.ak baino.
- Bestalde, 23. galderak erakusten du bitarterik handiena, aztergai hartu ditugun artean. Baina, hala ere, bigarren koartila 2tik hurreago dauka 3tik baino; laugarren koartilaren muga 3an dago. Beraz, uler dezakegu puntualtasunen baten gora beheran, hori ere bariazio gutxiago duten galderen artekoa dela, nahiz eta besteek baino kopuru handiagoa hartu neurraldiren batean.
Ondoriotzat har dezakegu 6., 18., 22. eta 32. galderetan bariazio handiagoa ikusi dela besteetan baino.
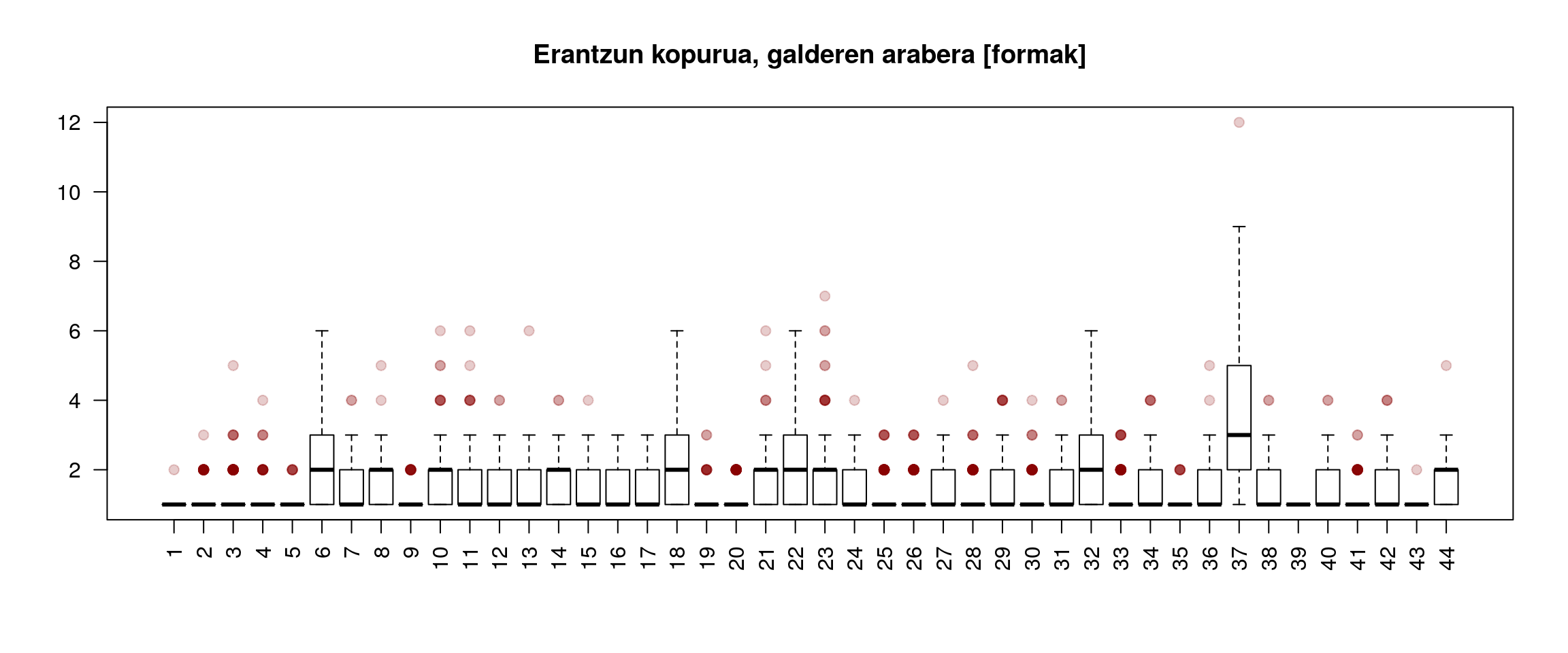
Kutxa diagramen azterketa eginda, ematen du aztertu diren galderen artean 37.ak duela bariaziorik handiena eta bigarren maila batean ematen du 6.a, 18.a, 22.a eta 32.a daudela; goragoko azterketan nabarmendutako horietxek. Bariaziorik baxuena, berriz, 39. galderak duela ematen du.
Azterketa sakonagoa egin genezake aldagaien deskriptore estatistikoak aztertuta. Segidan eskaintzen da lehenengo berrogeita lau galderetan hartutako erantzun kopuruen zenbakizko deskribapena.
| Galdera | \(\bar{x}\) | \(\sigma\) | \(Me\) | Moztutako \(\bar{x}\) | heina | skew |
|---|---|---|---|---|---|---|
| 1 | 1.01 | 0.08 | 1 | 1.00 | 1 | 11.79 |
| 2 | 1.14 | 0.37 | 1 | 1.05 | 2 | 2.39 |
| 3 | 1.30 | 0.59 | 1 | 1.19 | 4 | 2.63 |
| 4 | 1.14 | 0.46 | 1 | 1.02 | 3 | 3.60 |
| 5 | 1.04 | 0.20 | 1 | 1.00 | 1 | 4.56 |
| 6 | 2.03 | 1.09 | 2 | 1.87 | 5 | 1.34 |
| 7 | 1.33 | 0.59 | 1 | 1.22 | 3 | 2.01 |
| 8 | 1.87 | 0.70 | 2 | 1.81 | 4 | 0.79 |
| 9 | 1.09 | 0.29 | 1 | 1.00 | 1 | 2.84 |
| 10 | 1.78 | 0.98 | 2 | 1.62 | 5 | 1.47 |
| 11 | 1.60 | 0.95 | 1 | 1.42 | 5 | 1.77 |
| 12 | 1.41 | 0.65 | 1 | 1.29 | 3 | 1.62 |
| 13 | 1.47 | 0.72 | 1 | 1.34 | 5 | 2.31 |
| 14 | 1.72 | 0.80 | 2 | 1.63 | 3 | 0.71 |
| 15 | 1.41 | 0.61 | 1 | 1.32 | 3 | 1.38 |
| 16 | 1.42 | 0.67 | 1 | 1.28 | 2 | 1.30 |
| 17 | 1.32 | 0.55 | 1 | 1.22 | 2 | 1.51 |
| 18 | 2.17 | 1.09 | 2 | 2.03 | 5 | 0.88 |
| 19 | 1.08 | 0.32 | 1 | 1.00 | 2 | 4.14 |
| 20 | 1.19 | 0.39 | 1 | 1.11 | 1 | 1.58 |
| 21 | 1.88 | 0.89 | 2 | 1.78 | 5 | 1.24 |
| 22 | 2.09 | 1.26 | 2 | 1.91 | 5 | 0.98 |
| 23 | 1.94 | 1.11 | 2 | 1.75 | 6 | 1.77 |
| 24 | 1.32 | 0.60 | 1 | 1.21 | 3 | 1.85 |
| 25 | 1.26 | 0.51 | 1 | 1.16 | 2 | 1.80 |
| 26 | 1.27 | 0.52 | 1 | 1.17 | 2 | 1.74 |
| 27 | 1.47 | 0.66 | 1 | 1.36 | 3 | 1.22 |
| 28 | 1.26 | 0.58 | 1 | 1.14 | 4 | 2.95 |
| 29 | 1.57 | 0.81 | 1 | 1.42 | 3 | 1.39 |
| 30 | 1.19 | 0.49 | 1 | 1.08 | 3 | 2.87 |
| 31 | 1.46 | 0.68 | 1 | 1.33 | 3 | 1.43 |
| 32 | 2.14 | 1.25 | 2 | 1.93 | 5 | 1.28 |
| 33 | 1.25 | 0.52 | 1 | 1.14 | 2 | 1.97 |
| 34 | 1.49 | 0.76 | 1 | 1.33 | 3 | 1.52 |
| 35 | 1.04 | 0.20 | 1 | 1.00 | 1 | 4.56 |
| 36 | 1.43 | 0.71 | 1 | 1.30 | 4 | 1.88 |
| 37 | 3.60 | 1.97 | 3 | 3.43 | 11 | 1.02 |
| 38 | 1.58 | 0.67 | 1 | 1.49 | 3 | 0.99 |
| 39 | 1.00 | 0.00 | 1 | 1.00 | 0 | NaN |
| 40 | 1.47 | 0.70 | 1 | 1.33 | 3 | 1.39 |
| 41 | 1.14 | 0.39 | 1 | 1.04 | 2 | 2.67 |
| 42 | 1.60 | 0.76 | 1 | 1.48 | 3 | 1.09 |
| 43 | 1.01 | 0.08 | 1 | 1.00 | 1 | 11.79 |
| 44 | 1.65 | 0.69 | 2 | 1.55 | 4 | 1.09 |
Irudi-analisia, bataz bestekoaren arabera
Bataz bestekoaren araberako hurrenkeran aurkezten dira goiko taulako datuak. Lehenengo irudiak batezbestekoaren hurrenkera eta bataz besteko balioen irudikapena ikusten da; bigarrenean desbiderapen tipikoa, eta hirugarrenean balio zentrala. Bigarren taldean, lehenengo irudiakmoztutako batez bestekoa irudikatzen da, bigarrenean baliorik baxuena eta altuenaren arteko heina, eta hirugarrenean, banaketaren alborapena.
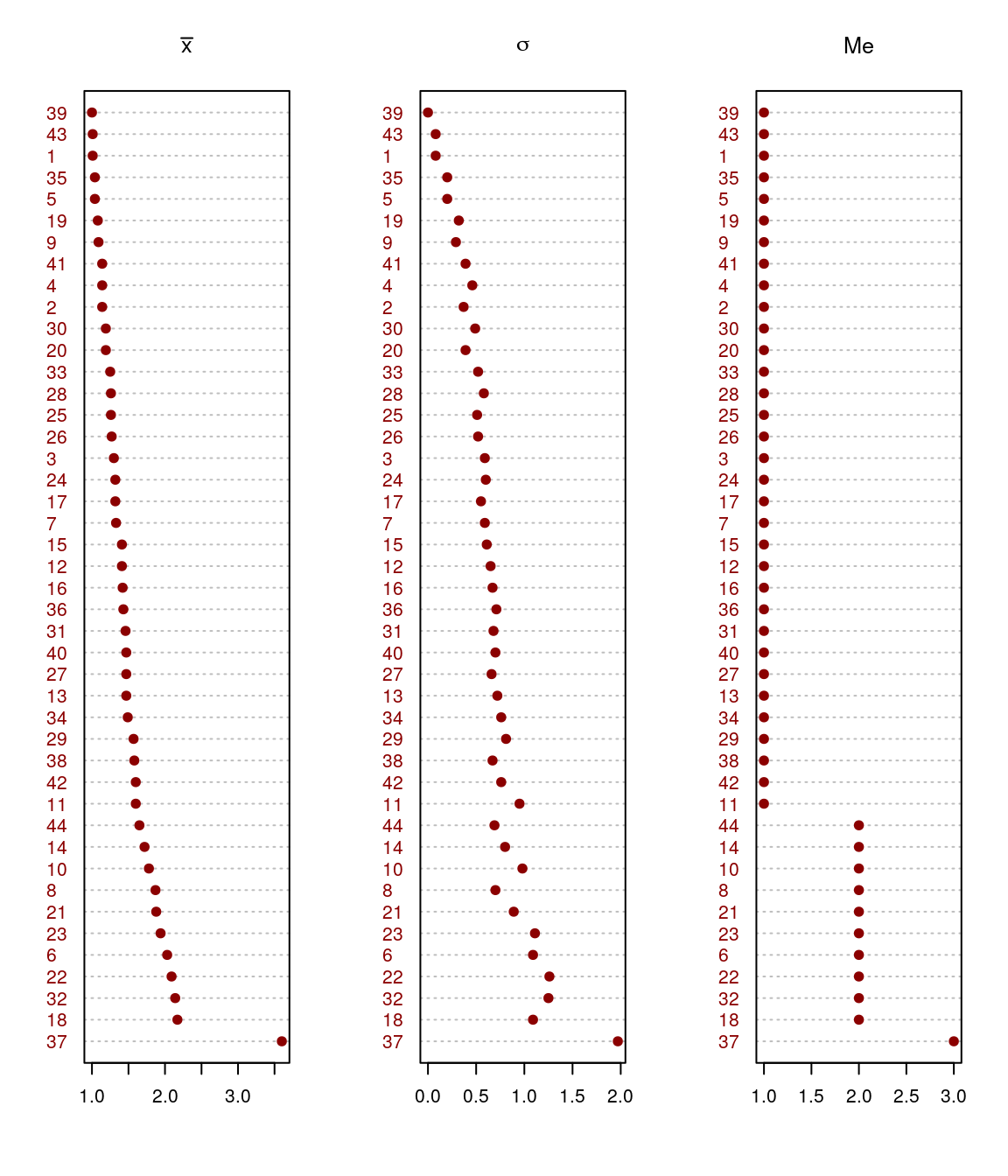
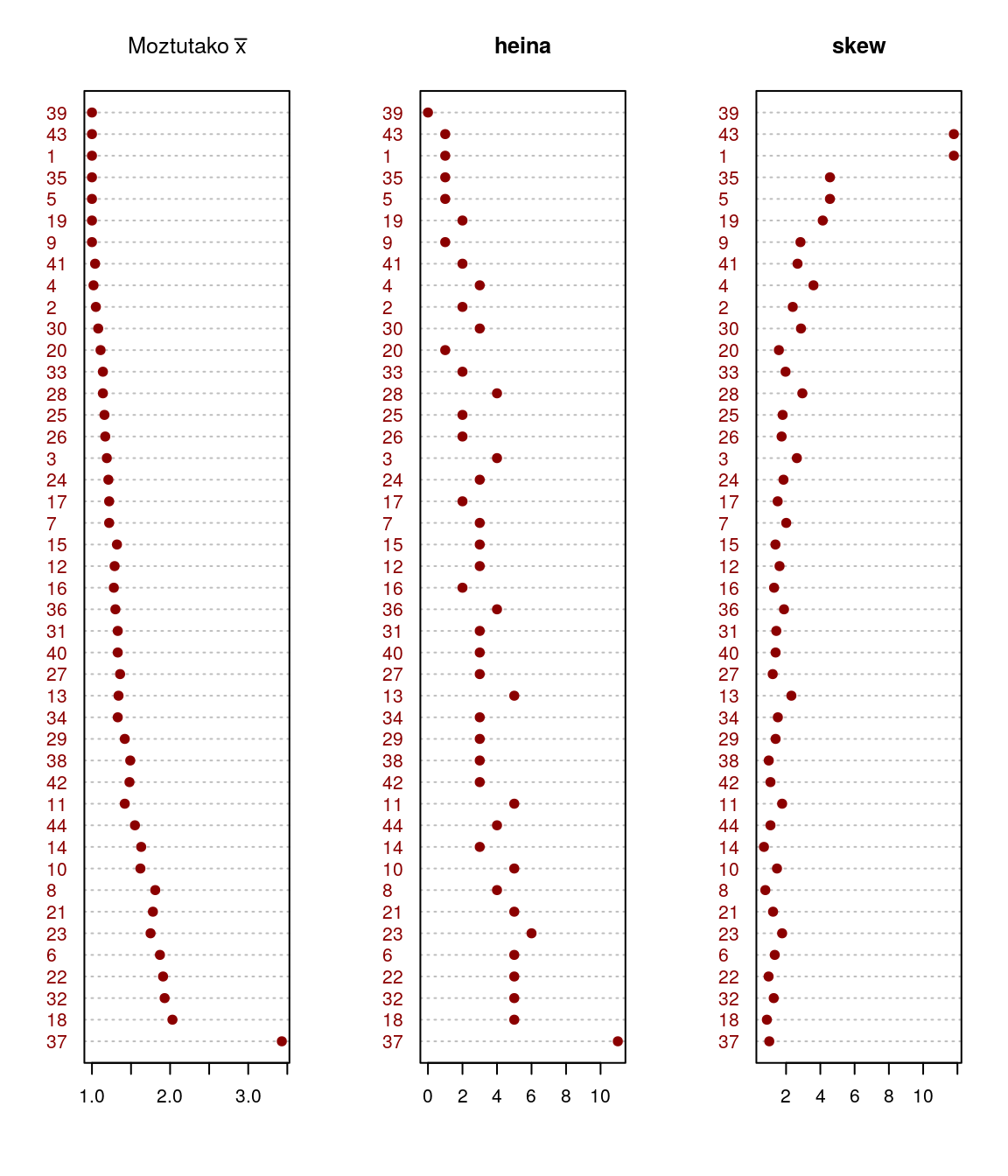
Azterketarako hurrerapeneko azken grafikoen analisiak datuen banaketa koherentea erakusten du, ñabardurarik ñabardura.
Argi dago grafikoetan gorengo irudikatutako galderek dutela bariaziorik handiena. horietan ikusten da bataz besteko baliorik altuenak, moztua izan zein ez. Horietan ere ikusten dira balio zentralik altuenak, desbiderapen neurri handienak edo handienetarikoak hor kokatzen dira; heinik handienak ere hor ere badaude, zein ezkerrerako alborapenik baxuena datu horietan aurkitu dira.
Beraz, aztertutako 44 galderen erantzunaren aniztasunari begiratuta, ematen du bariaziorik altuena goiko elementuek dutela esan dezakegula, erratzeko beldurrik gabe.
Hurrengo baterako, interesgarria litzateke ezaugarrien muga antzemateko irizpideak ere ematea.Oraingoan lehenengo laurdenari begiratuko diogu. Hauek dira, honen arbera, bariaziorik handiena duten galderak: 37, 18, 32, 22, 6, 23, 21, 8, 10, 14, 44.
Bariazio handiena, elementu guztiak kontuan izanda:
Bariazioa aztertzeko erabili ditugun teknikak izan dira: batez bestekoa (zuzena eta moztua), desbiderapen standarra, gutxieneko eta gehieneko balioen arteko balioa, erdiko balioa (mediana) eta alborapena. Azken kasu hori, alborapenarena, hartu da kontuan, baina aldrabesezko ordenan, hau da, zenbat eta balio baxuagoa izan, orduan eta ezkerrerako alborapen gutxiago izango duenez, balioen baxutasunaren arabera aztertu da
Deskribatzaile bakoitzaren arabera egindako sailkapeneko lehenengo laurdenen batura: 1, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 2, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 3, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 4, 40, 41, 42, 43, 44, 5, 6, 7, 8, 9.
Deskribatzaile guztietan lehenengo laurdenean agertzen diren galderak: 10, 18, 21, 22, 23, 32, 37, 6.
Esan bezala, honetan aurkezten diren bariazio handiko neurriak batzuk baino ez dira eta adizio zein intersekzio ikuspegian aurkezten dira. Erabakitzeko dago, ordea, zein balio mota komeni den erabiltzea eta zergatik.
Bariazio handia beste konfigurazio batzuetatik
Betiere, ariketa honetan lematizatuta ageri diren erantzunetan baino ez gara ari (lehenengo 44 galderetan).
Lemen bariazioa galderetan
Deskribatzaile bakoitzaren arabera egindako sailkapeneko lehenengo laurdenen batura: 1, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 2, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 3, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 4, 40, 41, 42, 43, 44, 5, 6, 7, 8, 9.
Deskribatzaile guztietan lehenengo laurdenean agertzen diren galderak: 18, 21, 22, 23, 32, 37, 6.
Lemen bariazio handia herrietan
Deskribatzaile bakoitzaren arabera egindako sailkapeneko lehenengo laurdenen batura: denak.
Deskribatzaile guztietan lehenengo laurdenean agertzen diren galderak: Errigoiti, Etxebarri, Fika, Mungia, Orozko, Zaratamo.
Formen bariazio handia herrietan
Deskribatzaile bakoitzaren arabera egindako sailkapeneko lehenengo laurdenen batura: denak.
Deskribatzaile guztietan lehenengo laurdenean agertzen diren galderak: Altzuruku, Errigoiti, Etxebarri, Ezterenzubi, Fika, Mungia, Orozko.
Erreferentziak
Dialektologia batzordea. 2008. Euskararen Herri Hizkeren Atlasa. Bilbo: Euskaltzaindia.